Casio
AS 3.14 Probability Distributions
Online resources
3.14 Probability Distributions A (The Stats Learning Centre)
3.14 Probability Distributions B
3.14 probability Distributions C
3.14 Probability Distribution D
Activities
Binomial Distribution
Poisson Distribution
Normal Distribution (basic)
Approx Binomial with Normal
Distributions practice 1
1. Seeds
are planted in rows of six. After 14
days the number of seeds which have germinated in each of the 100 rows is
noted. The results are shown in the
table:
Number
of seeds germinating
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
Number
of rows
|
2
|
1
|
2
|
10
|
30
|
35
|
20
|
Find the theoretical frequencies of 0, 1, 2, …, 6
seeds germinating in a row, using an associated theoretical distribution. Justify your use of the theoretical
distribution.
2. The
number of telephone calls received per minute at the switchboard of a certain
office was logged during the period 10 a.m. to noon on a working day. The
results were as in the following table. f is the number of minutes with x
calls per minute.
x calls per
minute
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
f
|
7
|
18
|
27
|
28
|
20
|
11
|
5
|
a.
Calculate the mean number of calls per minute. Select an appropriate theoretical
distribution to represent this situation, and justify your choice. Use the theoretical distribution to find for
the following working day:
b. The probability that two or more calls will
be received during any one minute.
c. The probability that no calls will be
received during any one minute.
3. The number of accidents notified in a
factory per day over a period of 200 days gave rise to following table:
Number
of accidents
|
0
|
1
|
2
|
3
|
4
|
5
|
Number
of days
|
127
|
54
|
14
|
3
|
1
|
1
|
a.
Calculate the mean number of accidents per day
b. Select a suitable theoretical distribution to
represent this situation and justify its use.
What is the probability that there will be more than 5 accidents in a
day?
c. Of the items produced by a machine,
approximately 3% are defective and those occur at random. What is the
probability that, in a sample of 144 items, there will be at least two which
are defective?
Number of faulty items
|
0
|
1
|
2
|
3
|
4
|
5
|
Frequency
|
297
|
90
|
10
|
2
|
1
|
0
|
4.
In a large batch of items from a production line the probability that an item is faulty is p. 400 samples, each of size 5, are taken and the number of faulty items in each batch is noted.
In a large batch of items from a production line the probability that an item is faulty is p. 400 samples, each of size 5, are taken and the number of faulty items in each batch is noted.
a. Estimate p
from the frequency distribution given in the table.
b. Select a
theoretical distribution to model this situation, and justify its use. Use it to estimate the number of samples of
size five which would be expected to have more than one faulty item, if 600
samples were taken from the production line.
5. The number of emergency admissions each
day to a hospital varies. The mean
number of admissions is 2 with a standard deviation of 1.5. Select a suitable theoretical distribution to
model this situation, justify your choice, and use the distribution to answer
the following:
a. Evaluate the probability that on a particular
day, there will be no emergency admission.
b. At the beginning of one day the hospital has
5 beds for emergencies. Calculate the probability that this will be an
insufficient number for the day.
c. Calculate the probability that there will be
exactly three admissions on two consecutive days.
6. A firm selling electrical components
records the number of new orders received over a period of 150 days
Number
of new orders
|
0
|
1
|
2
|
3
|
4
|
Number
of days
|
51
|
54
|
36
|
6
|
3
|
a. Find the average number of new orders per day
b. Use an appropriate theoretical distribution
to calculate the probability that there will be 5 or more orders in a day. Justify your choice of distribution.
c. The firm packs the electrical components in
boxes of 60. On average 2% of the components are faulty. What is the chance of
getting more than two defective components in a box?
7. On
average 20% of the bolts produced by a machine in a factory are faulty. Samples of ten bolts are to be selected at
random from the bolts produced that day.
a. Calculate the probability that, in any one
sample, two or fewer bolts will be faulty.
b. Find the expected value and standard deviation
of the number of bolts in a sample which will not be faulty.
c. State any assumptions you have made in
answering this question, and comment on whether the assumptions were valid.
8. a.
National records for the past 100 years were examined to find the number of
deaths in each year due to lightening. The most deaths were in any year were
four which was recorded once. In 35 years no death was observed and in 38 years
only one death. The mean number of deaths per year was 1.00. Draw up a
frequency table of the number of deaths per year, and estimate the
corresponding expected frequencies for an associated theoretical distribution
having the same mean.
b. Justify your
choice of theoretical distribution to model the number of deaths per year.
9. In one
trial of an experiment a certain number of dice are thrown and the number of
sixes rolled is recorded. The dice are
all biased the same way, and the probability of getting a six in one throw is p.
The results of sixty trials are shown in the table.
Number
of sixes rolled
|
0
|
1
|
2
|
3
|
4
|
>
4
|
frequency
|
19
|
26
|
12
|
2
|
1
|
0
|
Choose a theoretical distribution to model this situation. By comparing these results with those expected for the theoretical distribution, estimate the number of dice thrown in each trial, and the value of p.
Time
(am)
|
status
|
7:00
– 7:32
|
idle
|
7:32
– 8:20
|
active
|
8:20
– 8:30
|
idle
|
8:30
– 9:30
|
active
|
9:30
– 10:00
|
idle
|
10. The
manager of a processing plant noticed during the course of a morning that one
of her employees was often idle. She
decided to record when the employee was active or idle over a 3 hour
period. The results are given in the
table.
a) If the
manager had walked through the processing plant at a random time between 7:00
am and 10:00 am, determine the probability that she would have found the
employee idle.
b) If the
manager had randomly observed the employee for 6 one-minute time periods
between 7 and 10 am, justify the use of the binomial distribution to model the
situation.
c) Find the
probability that the employee would have been idle for all 6 random one-minute
observations.
d) Find the
probability that the employee would have been active less than half the time.
Distributions practice 2
QUESTION ONE
According to a food crop inspector, a particular
potato disease occurs randomly and independently in plants. He keeps records of the frequency of the
disease when he visits farms, and has counted the diseased plants per hectare
in 50 hectares of potatoes:
Diseased plants
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
Number of hectares
|
11
|
16
|
12
|
7
|
3
|
0
|
1
|
a) The
inspector wants to inspect any potato fields with more than 4 diseased plants
per hectare. Use a theoretical
distribution to model the situation and find the probability that a randomly
selected hectare of potato crops has more than four infected plants. Justify your choice of theoretical
distribution and explain any assumptions you have made.
b) Of the crop farms
in the region, 18% have potato crops. As
part of an audit, the inspector randomly selects 12 crop farms to visit in that
region. Calculate the probability that
two of twelve randomly selected farms will have potato crops.
QUESTION TWO
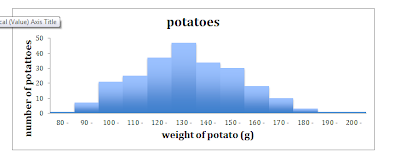
A farmer takes a random sample of the weight of 235
potatoes produced on his farm.
a) Estimate the
mean and standard deviation of the weight of a potato from the farm.
(b) Suggest a suitable theoretical distribution to
model this situation. Justify your
choice and explain any asssumptions you have made.
(c) One hundred and fifty grams is considered the
perfect size for a potato, and the farmer gets paid more for potatoes within 25
grams of that weight. What percentage of
his crop is likely to be between 125g and 175g?
(d) Of all the potatoes produced on the farm, the
lightest 5% get used to feed the pigs.
What is the maximum weight of a potato likely to be used as pig feed?
(e) At the farmer’s market, the farmer sells bags of
potatoes with a minimum weight of 1kg.
Usually 7 potatoes is the right number to fill a bag with just over 1kg,
but about 1 in 20 bags only need 6 potatoes.
If someone buys 5 bags of potatoes, what is the probability that they
will have at least 32 potatos.
QUESTION THREE
In another region the inspector notices that some of
the potatoes are a very unusual shape. Further studies suggest that the
occurrence of these unusually-shaped potatoes appears to be entirely random.
The inspector discovers that potatoes with the very unusual shape occur on
average in one potato plant per hectare in the region.
Over a two-day period the inspector is checking for
the presence of the unusually-shaped potatoes in plants from the region. On
each day, an area of five hectares will be randomly chosen, and the plants
studied.
What is the probability that on both days the
inspector finds no plants with the unusually-shaped potatoes?
QUESTION FOUR
The company that employs the food crop inspectors has
a variety of procedures in place to ensure that all tests carried out to check
the quality of the potatoes are accurate. The inspector carries out testing on
the basis that 1.8% of test results are misinterpreted. A random sample of 200 test results is
studied.
One of the company managers states that if more than
three of the test results in the sample are found to have been misinterpreted,
then all of those potato crops will need to be retested.
Let the random variable X represent the number of
misinterpreted test results in the sample.
(a) State the name of a theoretical distribution which
could be used to model the number of misinterpreted test results in the
sample. Justify your choice of
distribution.
(b) Calculate
the probability that no more than three of the 200 test results are
misinterpreted.
Simulation
Distributions and the broken stick
Stan challenges Ruby with the famous
“broken stick” probability problem. If
you break a stick at two random places, what is the probability that the pieces
can be arranged into a triangle?
1.
Ruby can’t see a way to solve the problem using maths, so she decides to
simulate breaking a 100cm stick 200 times, using excel, and gets the following
distribution of lengths for the longest piece of stick (-40 means ≤ 40cm, -50
means 40cm < length ≤ 50cm, etc).
a)
Does the graph above give you enough information to estimate a solution
to the problem? If not, what other
information do you need?
b)
Are there limits on how short or how long the longest piece of stick
could be? If so, what are the limits? If not, explain why not.
c)
Estimate the mean and standard deviation of the distribution graphed
above.
d)
Is there a theoretical distribution you could use to model the length of
the longest piece of stick? If so,
justify your choice and use it to estimate the
probability that the pieces of stick can be used to make a
triangle. If not, explain why not and estimate
the probability using another method of your choice.
e) Solve the problem mathematically. Compare your answer to your estimate from
part (c) above and comment on similarities and/or differences.
Triangular Distribution
Triangular Distribution notes
Sigma homework book P141 Question 4 Triangular distribution
Uniform Distribution
Uniform Distribution notes
2013 Sample paper and assessment schedule
Click here
Please note: I disagree with the NZQA assessment schedule on Question 3 (c) and I am seeking clarification on this question. I think it models the normal distribution (not the triangular distribution) as it is not mentioned in the question that the sales will not exceed $1000.









No comments:
Post a Comment